Dynamic programming – Backtracking algorithm usage in Permutation and Combination

Introduction

In earlier posts, I have explore various problems that employ backtracking algorithm. The backtracking algorithm is particularly useful when:

• the problem could be described as a tree,
• each node is a subproblem,
• and the leaves are the base case and provide solution.
• forward logic allows going deeper to child nodes and appropriate recursive calls could be used.
• backward logic happens after the recursive call returns results.
• the results from child nodes are combine at parent nodes.

Backtracking is a special Divide and Conquer technique that is very intuitive. In this post, I apply the algorithm to find the permutation and combination k items from a set of n values.

Concepts Permutation vs Combination

Permutations:

• A permutation is an arrangement of all or part of a set of objects in a specific order.
• The items in subsets cannot be repeated.
• The order of arrangement of items in the subset are important.
• Total permutation is calculated as:

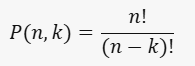
Combinations:

• A combination is a selection of items from a set where the order of the items does not matter.
• The item in subsets cannot be repeated.
• Total combination is calculated as:

Implementation

Permutations

The following illustrate a permutation of a set of 3 items (n=3, k=3). The red boxes and arrows are invalid paths.

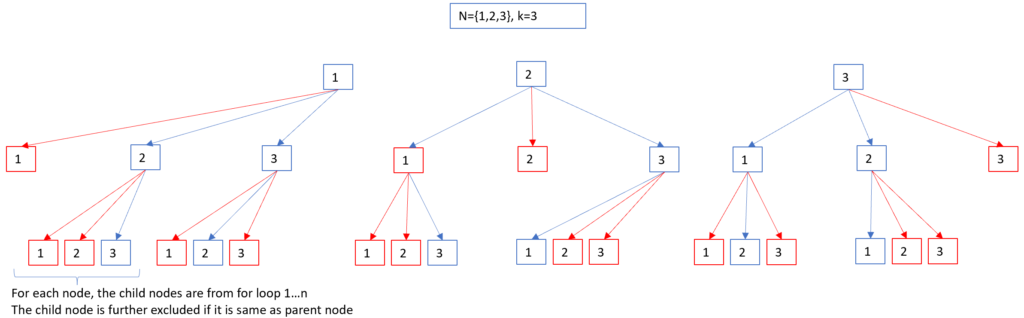
From the above illustration, we can see that:

• each node, except leaf, will have child nodes in full range from 1..n.
• exception is if childNode = currentNode.
  • Note [1,2,1] is not correct permutation => if currentItem is 2, and nextItem is 1, the simple comparison above will result in incorrect permutation.
  • create a flag to mark that the item could have been used in the subset. Backtracking logic should be provided and unmark the item when backtracking.

Key points to remember when implementing backtracking:

• base condition.
• if for loop is needed for multiple branches.
• forward logic
• backward logic.

Pseudo codes:

Provide base logic to identify last node
For (int nextItem=1; nextItem<=n; nextItem++){
       if (nextItem != currItem){
	proceed to nextItem by by passing next item to recursive call
                 provide backtracking logic to go back to parent node, (currItem)
       }
}

Full Codes:

In the following implementation, markCandidate vector is used to mark when the item is already pushed into permutation subset.

#include <iostream>
#include <vector>
using namespace std; 

class Solution {
    
    void formPermutation(vector<vector<int>>&comb, vector<int>& curr, vector<bool>& markCandidate, int firstItem, int n, int k){
        // base case:
        if (curr.size()==k){
            comb.push_back(curr);
            return;
        }
        for (int nextItem = 1; nextItem <= n ; nextItem++){
            if (markCandidate[nextItem] != true){
                // forward logic
                markCandidate[nextItem] = true;
                curr.push_back(nextItem);                   
                formPermutation(comb, curr, markCandidate, nextItem, n, k);
                markCandidate[nextItem] = false;
                // backtracking logic
                curr.pop_back();
            }
        }
    }
public:
    vector<vector<int>>permutation(int n, int k) {
        vector<vector<int>> result; 
        // 1.pick 1, marked 1: the combination should be [1 2][1 3].... 
        // 2.=> for loop 1...n recursive to push 2, 3, dont pick 1 [1 1] because it is marked.
        // 3. backtrack for every iteration pick 2, : [1 2]  -- backtrack --[1 3] -- backtrack [1 4]
        // 4. after i=n, backtrack further, pick 2, : [2 1] should be taken
        vector<int> curr;
        vector<bool> markCandidate (n+1,false);
        for (int firstItem = 1; firstItem <= n ; firstItem++){
            curr.push_back(firstItem);
            markCandidate[firstItem] = true;
            formPermutation(result, curr, markCandidate, firstItem, n, k);
            curr.pop_back();
            markCandidate[firstItem] = false;
        }
        return result; 
    }
};

int main(){
    Solution sol;
    int n=3, k=3;
    vector<vector<int>> result; 
    result = sol.permutation(n,k);
    for ( int row = 0; row < 6; row++){  // total combination is 3!/(3-3!) =6
        for (int col = 0; col <k; col++){
            cout<< result[row][col] <<" ";
        }
        cout<<endl;
    }
}

Combinations

The following illustrate the result of combination when n=3,k=3. Red indicates invalid path.

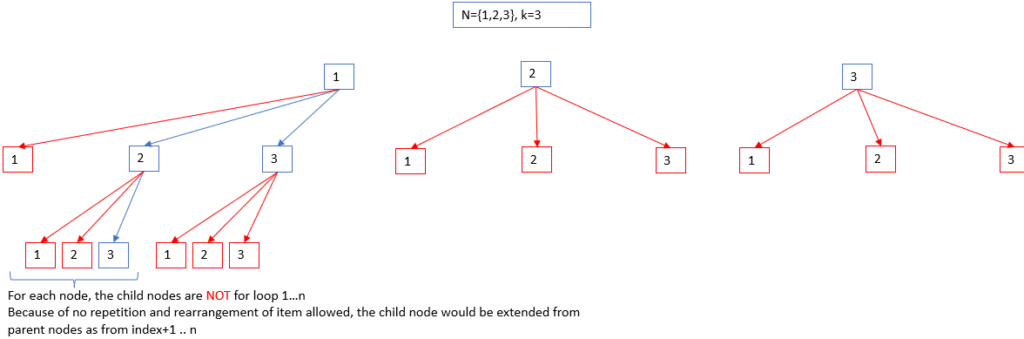
From the above illustration, we can see that:

• each node, except leaf, will have child nodes that starts from currIndex+1 to n
• There is no need to check if currNode != nextNode, because the nextNode is identified by currIndex+1. Thus there will be no repetition.
• Forward logic: should push the nextNode to combination vector.
  • Suppose we are at node [1], the current combination is empty []. Since we assign nextNode = currentNode in our for loop, the term nextNode actually saves the values of the items in the parent node.
  • To proceed to child node, make recursive call where nextNode=nextNode+1.
• Backward logic:
  • should pop out the nextNode from combination vector. Suppose we are at node [2], after proceeding to node [3], combination vector is [1,2,3]. On backtrack, we pop out [3]
  • At the point, we also have the nextNode value being [2]. nextNode actually saves the node values that could be retrieved on backtracking.
• Base condition: leaf node returned when combination vector size equals k.

C++ implementation

class Solution {
    void formCombination( vector<vector<int>>& result, vector<int>&currCombination,  int n, int k, int currItem){
        // base condition:
        if (curr.size()==k){
            result.push_back(curr);
            return;
        }
        
        for(int nextItem = currItem; nextItem<=n; nextItem++){
            //forward logic
            currCombination.push_back(nextItem);
            formCombination(comb, currCombination, n, k, nextItem+1);
            //backward logic
            currCombination.pop_back();
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        vector<vector<int>> ans;
        int start = 1;
        vector<int> currCombination;
        formCombination(ans, currCombination,n, k, start);
        return ans;
    }
};