Sort Algorithm 3 – Merger Sort

Introduction

Merge sort is a kind of a divide and conquest technique. Unlike Heap Sort, where we employ heap data structure to sort the array, for Merger Sort, we recursively bisect the input array to smaller subarrays, sort them and then recombine the subarray. This post will elaborates the technique to implement Merger Sort.

Concepts

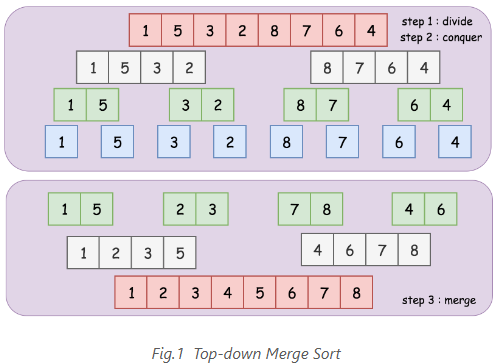
Merger Sort follows the divide and conquest technique. The algorithm includes 3 basic steps:

1. Divide the given unsorted list into several sublists,   (Divide)
2. Sort each of the sublist recursively.  (Conquer)
3. Merge the sorted sublist to produce new sorted list.  (Combine)

• Time Complexity: O(nlogn)
• Space Complexity: O(1)

Implementation

There are slightly different techniques to implement the algorithm. Generally, We don't have 3 functions for 3 steps, but 2 functions and share the work in each step. We have 2 main functions: mergeSort and merge.

• mergeSort is the initial call and performs step 1, step 2.
  • partition the input array into left and right subarrays of equal size.
  • recursively calls itself to partition the subarrays until there is only 1 element (base case).
• merge performs step 2 and 3, combining sorted subarrays.
  • When combining the subarrays, it compare each items of the left and right subarray.
  • Smaller items from either arrays are filled first, then remaining item from left array, and then right array are filled.

#include <iostream>
#include <vector>

using namespace std;

// Sort and Merges two subarrays of vec.
void merge(vector<int>& parentVect, vector<int>& left, vector<int>& right) {
    int parentIndex = 0, leftIndex = 0, rightIndex = 0;
    int leftBound = left.size();
    int rightBound = right.size();

    // Merge the two subarrays
    while (leftIndex < leftBound && rightIndex < rightBound) {  
        if (left[leftIndex] <= right[rightIndex]) {
            parentVect[parentIndex] = left[leftIndex];  
            leftIndex++;
        } else {
// Ig: [5,4] [1,7]  => L=[5,4] move right index, R=[7], parent=[1]
            parentVect[parentIndex] = right[rightIndex];  
            rightIndex++;
        }
        parentIndex++;
    }

    // Copy the remaining elements of left[], if any
    while (leftIndex < leftBound) {
        parentVect[parentIndex] = left[leftIndex];
        parentIndex++;
        leftIndex++;
    }

    // Copy the remaining elements of right[], if any
    while (rightIndex < rightBound) {
        parentVect[parentIndex] = right[rightIndex];
        parentIndex++;
        rightIndex++;
    }
}

// Divide the input arrays to subarrays until size = 1
void mergeSort(vector<int>& parentVect) {
    if (parentVect.size() <= 1)
        return;

    int leftSize = parentVect.size() / 2;
    int rightSize = parentVect.size() - leftSize;

    // Create temporary vectors
    vector<int> leftVect(leftSize), rightVect(rightSize);

    // Copy data to temporary vectors
    for (int i = 0; i < parentVect.size(); i++) {
        if (i < leftSize)
            leftVect[i] = parentVect[i];
        else
            rightVect[i - leftSize] = parentVect[i]; 
    }

    // Recursively break up the arrays
    mergeSort(leftVect);
    mergeSort(rightVect);

    // Merge the sorted halves
    merge(parentVect, leftVect, rightVect);
}

int main() {
    vector<int> vec = {12, 11, 13, 5, 6, 7};

    // Sorting vec using mergesort
    mergeSort(vec);

    for (auto i : vec)
        cout << i << " ";
    return 0;
}