Sort Algorithm 2 – Heap Sort

Introduction

Selection Sort, Bubble Sort, Insertion Sort are simple but not very fast due to double nested for loops. In this post, Heap Sort is studied.

Heap concepts

• Heap is a complete binary tree.
  • a full binary tree: every node has either 2 children or zero children.
  • a perfect binary tree: every node has 2 children. The total number of nodes is the maximum number of node for a binary tree of heigh h, which is 2^(h+1)-1.
  • a complete binary tree: a node may have only 1 child, it does not have the maximum number of nodes, all the children is in the left as much as possible.
  • binary search tree:
    • All values on the left subtree of a node should be less than the value of the node.
    • All values on the right subtree of a node should be greater than the value of the node.
    • Both the left and right subtrees must also be binary search trees.
  • red black tree: a kind of self balancing binary tree. In C++ STL, set and map are implemented as red black tree.

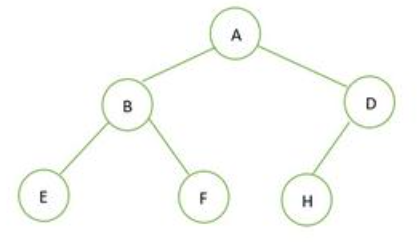
• For every node, the value of its children is greater than or equal to its own value (max heap) or less than or equal to the values of its children (min heap).
  • For max heap: the top of the heap or root is largest value.
  • For min heap: the top of the heap or root is the smallest.
• Heapify is a process to create a heap from an array, also convert an arbitrary binary tree into a heap. The algorithm will be further explained in Heap Sort section.
  • For any item at index i, its left child is at index 2i+1 and 2i+2.
  • For any item at index i, its parent is at index floor (i-1)/2
    • a complete binary tree, when filled to array, will have continuous allocated items.
  • Time complexity: O(n*logn).
    • build heap requires O(n)
    • heapify process requires O(logn)
• Insertion/Deletion: the process of adding a node into a heap. It may also involve swapping the root node with newly added node if the value is max/min. The insertion process then always needs "heapifying" process.
  • Time complexity: O(logn)

• Get Min/Max value time complexity is O(1) for Min/Max heap.

Min Heap vs Max Heap

	Max Heap	Min Heap
top node	The top root is the largest value	The top is the smallest
parent nodes	The parent node is greater than the left and right child nodes.	The parent node is smaller ...
STL implementation	priority_queue<int>maxH;	priority_queue < int, vector<int>, greater<int> > minH;

Heap sort

Heap sort is a process of building a Max Heap and repeatedly removing the min/max element to sort the array. The following 3 steps are basic for Heap Sort algorithm, using Max Heap.

• step 1: constructing a binary tree and then make it a max heap from the input.
• step 2: take the maximum element at index 0 (we know this is the maximum element because of the max-heap property) and swap it with the last element in the array (this element's proper place)
• step 3: decrease the heap size by 1. Heapify the remaining items again (go back to step 1). And do untill all items are sorted.

Time complexity: O (n*logn) :

• Remove the max element from heap costs O(logn)
• Build the heap costs O(n)

Code implementation:

The following implement Heap Sort using Max Heap and a top down order to heapify.

• It is topdown order because, heapify starts with index i = n / 2 - 1, and find left, right nodes.

// Function to heapify a subtree (in top-down order) rooted at index i.
void heapify(vector<int>& arr, int n, int i) {
    // Initialize largest as root 'i'.
    int largest = i; 
    int left = 2 * i + 1;
    int right = 2 * i + 2; 

    // If left child is larger than root.
    if (left < n && arr[left] > arr[largest]) {
        largest = left;
    }

    // If right child is larger than largest so far.
    if (right < n && arr[right] > arr[largest]) {
        largest = right;
    }

    // If largest is not root swap root with largest element
    // Recursively heapify the affected sub-tree (i.e. move down).
    if (largest != i) {
        swap(arr[i], arr[largest]); 
        heapify(arr, n, largest);
    }
}

void heapSort(vector<int>& arr) {
    int n = arr.size();
    // Step 1: Build heap; heapify (top-down) all elements except leaf nodes.
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(arr, n, i);
    }

    // Traverse elements one by one, to move current root to end, and
    for (int i = n - 1; i >= 0; i--) {
        // Step 2: swap the max element and the last element on graph
        swap(arr[0], arr[i]);
        // Step 3: call max heapify on the reduced heap.
        heapify(arr, i, 0);
    }
}

The following illustrate debug steps from the above codes, using sample test arr=[7,8,10]. The 3 steps are done in sequence:

• Although the array is already sorted, heap sort process will rebuild the max heap in step 1, which makes arr=[10,8,7] .
• Step 2 swaps arr[0] and min value which is arr[2]. The array is changed back to [7,8,10] and 10 is at its correct position.
• Step 3 rebuild max heap on new array [7,8] and doesn't make any new changes. Final result is [7,8,10]