Introduction
In earlier blog, Bit manipulation – Mask method, I gathered a few problem to demonstrate the powerful usage of bit masking. Mostly, I show the tricks with:
- a single bit 1 mask using
(num & 1) << i,num & (1 << i), - multiple bit 1 mask
Bit masking is used together with bitwise logic, shifting and arithmetic to provide intended operation or logic. So it is not used at a standalone method.
In this blog, I will focus on bit shifting, and explore several properties, or operation that gives some interesting results.
Concepts
- First of all, bit shifting is same as multiplying by two to some power:
num >> i = num * pow(2,i)
- left shift adds
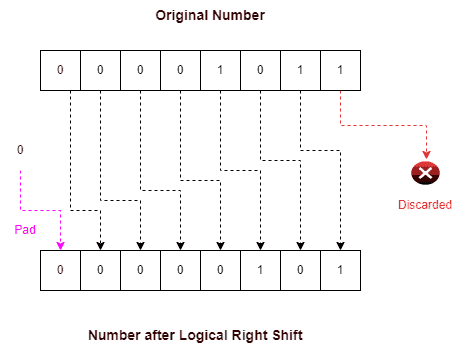
zerosto the rightmost - logical right shift
>>>addszerosto theleftmost of positive number.
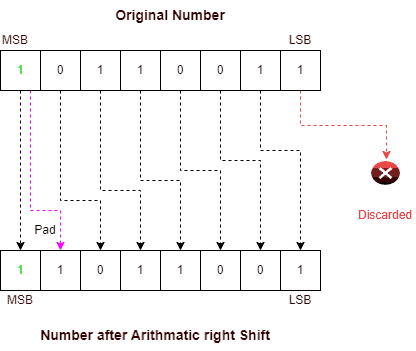
- arithmetic right shift
>>reserves the sign. If the number is negative, add i to the leftmost bit.
Problem Bitwise AND of all number in range
Firstly, we recognize that bitwise AND of all number in range between numberA and numberB is the common prefix of all binary representatives of those numbers. For example:
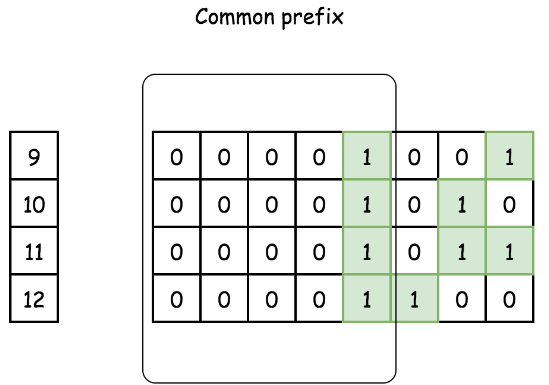
In order words, every bits on the right of the leftmost common one should be zero. Therefore, we could:
- shift the
numberAandnumberBrightward until 2 are equal. (not include equal case) - count the number of shifts.
- return result which is
(numberA >> count).numberAhere could be either1or0
class Solution {
public:
int rangeBitwiseAnd(int numberA, int numberB) {
int count = 0;
// find the common 1-bits
while (numberA < numberB) {
numberA >> = 1;
numberB >> = 1;
++count;
}
return numberA << count;
}
};Counting bit 1 for every number from 0 to n
The problem Counting Bits observes characteristics of binary representation when performing left shift. Using Dynamic Program and bit shifting offers faster calculation.
Brute force method with bit masking
- we can use bit masking to get the number of bit
1in each number. - we loop from 0 to n. For each number, calculate bit
1. This operation takesO(n).
Solution 1 with bit mask = 1
class Solution {
const int BITS = 32;
int countBit1(int n) {
int ans = 0;
for (int i = BITS - 1; i >= 0; i--) {
ans += (n & (1 << i)) ? 1 : 0;
}
return ans;
}
public:
vector<int> countBits(int n) {
vector<int> ans (n+1,0);
for (int i=0; i<=n; i++){
ans[i] = countBit1(i);
}
return ans;
}
};Solution with bit mask = num -1
public class Solution {
private int popCount(int x) {
int count;
for (count = 0; x != 0; ++count) {
x &= x - 1; // zeroing out the least significant nonzero bit
}
return count;
}
public int[] countBits(int n) {
int[] ans = new int[n + 1];
for (int x = 0; x <= n; ++x) {
ans[x] = popCount(x);
}
return ans;
}
}Dynamic Programming and Bit shifting solution
We made this observation:

We see that the bit counts of certain number depends on the previous count, which is the right shift's count. Thus this program can be solved by DP. The relation is then expressed by:
ans[num] = ans[num >> 1] + (i >>1)
class Solution {
public:
vector<int> countBits(int num) {
vector<int> ans (num+1,0);
for (int i = 0; i <= num; i++){
cout<<(i >> 1 )<<" "<<ans[0]<<endl;
ans[i] = ans[i>>1]+(i&1);
}
return ans;
}
};