Bit manipulation – Mask method

Introduction

In the blog How to convert unsigned integer to binary string representation, I have used the following codes to find the binary bit '1' at each position, and set it to '1' or '0'.

std::string binary = "";
for (int i = BITS - 1; i >= 0; i--) {
    binary += (num & (1 << i)) ? '1' : '0';
}

The logic num & (1 << i) basically performs and AND operation with a mask that has only bit 1 at position i-th. For example, if i=3 then 1<<3 is 0000 1000, which serves as a mask. Any value of num when ANDed with the mask, gives 1 or 0 at the bit i-th.

The method is called masking and could be used for variety of problems. The mask itself could be just 1<<i or anything suitable. In this blog, I gather a few to demonstrate its usage of bit masking.

Concepts:

When a mask is used with bitwise logic, it can perform certain "hacks":

AND logic

First of all, let makes sense of bitwise logic in common language. In order words, understand what the bitwise logic can allow us to do:

• pick a bit at i-th position with mask (1<<i).
  Eg: num & (1<<i)
• set the i-th bit with OR
• clear the i-th bit with AND
• toggle the i-th bit with XOR
• find the 1st '1' bit before '0'.
  Eg: if (num & (1<<i)) return i;
  or we can also do: num & (-num)
• Removes the rightmost bit '1':
  • (x-1) inverts all the bits till it encounters the lowest bit ‘1’
  • ANDing’ x with x-1 we get the lowest set bit stripped.

Eg: x = x & (x-1)
x =7 (0111) and x=6 (0110): 
0111 --> x
0110 --> x-1
------------
0110 --> bit 1 at position 0 changes to 0

• check if the number is power of 2: if (!(n&(n-1)) => n is power of 2
• check if the number is power of 4: a given num is a power of 2 if its sets bits are at even positions like i=0,2,4,6,8 and if it is already a power of 4

bool checkPowerOf4 (int num) {
    if (num==0) return false;
    bool powerOf2 =!(n&(n-1));
    bool mask     =!(n & 0xAAAAAAAA);
    return powerOf2 && mask;  
}

• Copy set bits in range from numberA to numberB.

int copyBitsInRange ( int numberA, int numberB, int left, int range){
     int mask   = 1ll << (right -left+1) - 1;
     int copy   = mask & numberA;
     int result = numberB | copy;
     return result;
}

XOR logic

Note that XOR is not the same as NOT( A OR B). In fact, a^b = (A’.B + A.B’).

• used to switch bits ON or OFF.
• reverts bits back to previous.
• invert a character from lowercase to uppercase by XOR with space.

char invertCase(char c){
    return (char)(c ^ ' ');
}

• used to implement sum of a+b. (todo: discuss in another blog).
• swap 2 numbers as we have property: A ^ B ^ B = A

void swap (int& numberA, int& numberB){
    numberA = numberA ^ numberB;
    numberB = numberB ^ numberA;
    numberA = numberA ^ numberB;
}

• find missing number in a continuous array. The array is expected to have continuous numbers from 0 to n, but there is a missing number while there is a duplicated.

int missingNumber(vector<int> &nums) {    //array in range 0..n with 1 number missing
    int ans=0;
    for (int i = 0; i<nums.size(); i++)   ans =ans ^ nums[i];
    for (int i=num.size()-1; i>=0; i--)   ans =ans ^ i;
    return ans;
}

• Toggle set bits in range from numberA

int toggleBitsInRange ( int numberA, int left, int range){ 
    int mask   = 1    << (right -left+1) - 1;   //extract the bits in range
    mask       = mask << (L-1);                 //put the bits in correct position of the mask      
    int result = numberB ^ mask; 
    return result;
}

• Check if 2 numbers have opposite signs a⊕b < 0

Problem reverse bits

The problem reverse bit asks to change the bits from left to right and vice versa. Note, it is not the same as inverting bits. The following illustrates expectation:

I will demonstrate 2 methods to solve this problem.

Using bit mask 1

• start from right to left: extract out a bit at position 0 from the num by masking (AND) it with bit 1: num &1
• shift the bit to the left by i-th steps.
• move to next bit of num on the left by shifting num to the left 1 step.

class Solution {
public:
    uint32_t reverseBits(uint32_t num) {
        uint32_t ret = 0;
        for (int i= 31; i>= 0; i--) {
            ret += (num & 1) << i;     // pick the rightmost and shift i-th
            num = num >> 1;            // shift num right to pick the next MSB
        }
        return ret;
    }
};

If we want to pick the left most bit, and move to the opposite left. The mask is then 1<<31

class Solution {
public:
    uint32_t reverseBits(uint32_t n) {
        uint32_t ret = 0;
        for (int i = 31; i >= 0; i--) {
            ret |= (n & (1 << 31)) >> i;  // pick the leftmost bit and shift i-th
            n = n << 1;                   // shift the num left 1 bit
        }
        return ret;
    }
};

Using multiple bit masks

Leetcode offers a fantastic solutions: we divide the original 32-bits into blocks with fewer bits via bit masking, then we reverse each block via bit shifting, and at the end we merge the result of each block to obtain the final result.

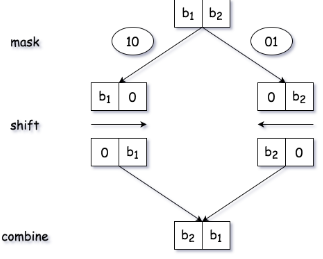
The problem is to decide the mask for each time.

• First we divide the 32 bits to half of 16 bits and swap them: n = (n >> 16) | (n << 16);

• Then we swap the left 8 bits and right 8 bits of each half of 16 bits above by using masks: 11111111000000001111111100000000 and 00000000111111110000000011111111
• And go on with 4 bits using masks:
  11110000111100001111000011110000 and 00001111000011110000111100001111
• and continue with 2 bits, 1 bits.

class Solution {
public:
    uint32_t reverseBits(uint32_t n) {
        n = (n >> 16) | (n << 16);
        n = ((n & 0xff00ff00) >> 8) | ((n & 0x00ff00ff) << 8);
        n = ((n & 0xf0f0f0f0) >> 4) | ((n & 0x0f0f0f0f) << 4);
        n = ((n & 0xcccccccc) >> 2) | ((n & 0x33333333) << 2);
        n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1);
        return n;
    }
};

Problem Minimum flips to make a OR b equal c.

Investigating OR result of (a OR b) and compare with c, bit by bit, we can come up with what needed to be changed at a and b. We use bit masking (1<<i) to extract the bits in 3 numbers.

Code:

class Solution {
public:
    int minFlips(int a, int b, int c) {
        int ans = 0;
        for (int i = 0; i < 32; i++) {
            // using bool to represent bit, true = 0, false = 1
            bool bitC = c & (1 << i);  
            bool bitA = a & (1 << i);
            bool bitB = b & (1 << i);

            if (bitC) {
                // c[i] = 1 and either a[i] or b[i] needs to be 1
                if (!bitA && !bitB) {
                    ans++;
                }
            } else {
                // c[i] = 0 and both a[i] and b[i] need to be 0
                if (bitA) {
                    ans++;
                }
                if (bitB) {
                    ans++;
                }
            }
        }
        return ans;
    }
};

Problem Constructing Minimum Bitwise Array

This problem Construct the Minimum Bitwise Array I could be solved by brute force method, but the bitwise method provides much faster, and even more intuitive solutions.

Brute force method

Brute force method just basically loops from 0 to any target and finds a number that fits requirement

(i | i+ 1) == num

class Solution {
    int findSmallest(int target) {

        for (int i=0; i<=target; i++){
            if ((i | i+1) == target)
            return i;
        }
        return -1;
    }
public:
    vector<int> minBitwiseArray(vector<int>& nums) {
        vector<int> ans(nums.size(), -1);
        for (int i =0; i< nums.size() ; i++){
            ans[i] = findSmallest(nums[i]);
        }
        return ans;
    }
};

Bitmask manipulation:

The following problem demonstrates the magic of OR logic and bit masking.

Using x=7, we investigate the bitwise operations:

x=7 in binary 0111, x+1=8 in binary: 1000
  0000 0111    7 is 8 which rightmost `1000` are flipped.
| 0000 1000    8 is 15 which rightmost `111` are reverted.
-----------
  0000 1111    ==> target = 15

Using x=44

x=44 in binary 0010 1101, x+1=45 in binary 0010 1100
  0010 1100
| 0010 1101
-----------
  0010 1101    ==> target = 45

Using x=67

x=67 in binary 0010 0011 , x+1=68 in binary 0010 0100 
  0010 0011   67 is 68 reverts back the rightmost `100`
| 0010 0100   68 is 45 that has all rightmost `11` flipped to `00` at the  
-----------
  0010 0111    ==> target = 45

We can recognise that pattern that helps us derive the bitwise logic:

1. flip all the right bits 1 before the first 1 followed by a 0 to get (x+1).
2. flip all the right most bits at the position found in (1) to get x.

Code:

class Solution {
public:
    vector<int> minBitwiseArray(vector<int>& nums) {
        vector<int> ans;
        for (int n : nums) {
            int bit = 0;
            // Find the first 0 bit
            while (n & (1 << bit))                              
                bit++;
            // (bit-1) goes to first 1 after 0 bit, reverts all those right bits from there. 
            ans.push_back(n > 2 ? n ^ (1 << (bit - 1)) : -1);   
        }
        return ans;
    }
};

Problem Binary number with alternating bits

The problem requests to check if a binary representation of a number has alternating bits.

This problem is marked as easy, but bit manipulating solution is very clever! It uses bit arithmetic as well as bit masking! It is based on the following observation:

             10101010101
         +    1010101010    ( input number >> 1 )
         ---------------
         =   11111111111
         &  100000000000
         ---------------
         =             0   

For C++, the problem has overflow issue that needs to be handled. INT in C++ has 32 bits and a limit range upto 2,147,483,647. Therefore,

• we cannot take 2,147,483,647 and add 1 like in the above logic. That number doesn't have alternating bits, thus we could just return false.
• any number that is multiplied by 2 and greater than 2,147,483,647 will cause overflow. The way to fix this is to cast 32 bits integer to 64 bits integer.

Code:

class Solution {
public:
    bool hasAlternatingBits(int number) {
        // Handle edge case for maximum unsigned int value
        if (number == INT_MAX) {
            return false;
        }

        // Use 64-bit integers to avoid overflow
        uint64_t tmp = static_cast<uint64_t>(number) + (static_cast<uint64_t>(number) >> 1);
        return (tmp & (tmp + 1)) == 0;
    }
};