Dynamic Programming – From Recursive to Tree Traversal

Introduction

Previously, I described various algorithms that grow from simple sorting problems:

• use double for loop to search through array: Sort Algorithm 1 – Selection vs Bubble vs Insertion Sort
• use divide and conquer techniques to search item through array. Recursive calls are used to continuously divide the big input array to smaller subarray. Sort Algorithm 3 – Merger Sort, Sort Algorithm 4 – Quick Sort
• apply backtracking technique Dynamic programming – Backtracking algorithm usage in Permutation and Combination as a special divide and conquer method to solve DP problems that could be describe as a decision trees. Subproblems are basically child nodes, the base problems are leaf nodes that return answer. The problem answer is returned by backtracking logic that traces back to top node or root node.

Since we have tree, it is also natural to have special Graph techniques, namely Depth First Search (DFS) and Breath First Search (BFS) that could address those problems. The techniques also have common template codes that ease the implementation.

In this post, I use the Unique Paths - LeetCode problem and solve it using backtracking and DFS technique. For each, I focus on visualizing the graph and how the codes could traverse the graph. For BFS, it is especially useful to visualize the effect of Flood Fill algorithm, which is basically BFS, and finally, a solution using iteration approach.

Backtracking

The following highlights the approach:

1. Base Case: If we reach the bottom-right corner (m-1, n-1), we return 1 as there’s one valid path.
2. Out of Bounds Check: If the current cell is out of the grid bounds, we return 0 as it’s not a valid path.
3. Recursive Calls: We recursively explore the paths by moving right (col + 1) and down (row + 1).
4. Sum of Paths: The total number of paths from the current cell is the sum of the paths obtained by moving right and down

#include <vector>

using namespace std;

class Solution {
private:
    int backtrack(int row, int col, int m, int n, vector<vector<int>>& memo) {
        // Base case: if we reach the bottom-right corner, there's one valid path
        if (row == m - 1 && col == n - 1) {
            return 1;
        }
        
        // If out of bounds, return 0 as it's not a valid path
        if (row >= m || col >= n) {
            return 0;
        }
        
        // If the result is already computed, return it
        if (memo[row][col] != -1) {
            return memo[row][col];
        }
        
        // Move right and down
        int rightPaths = backtrack(row, col + 1, m, n, memo);
        int downPaths = backtrack(row + 1, col, m, n, memo);
        
        // Store the result in memo and return it
        memo[row][col] = rightPaths + downPaths;
        return memo[row][col];
    }

public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> memo(m, vector<int>(n, -1));
        return backtrack(0, 0, m, n, memo);
    }
};

Optimization:

Backtracking algorithm alone could be costly and inefficient:

• Recursive calls takes space on call stack.
• Traversing every node/cells if efficient. (We can also observe that the cells could be adjacent multiple cells)

Using memoization helps. We could use 2D vector to store values of visited cell.

• Optimized time complexity: O(2^(M+N))
• Optimized space complexity: O(MxN)

Flood Fill - BFS

The following highlight the approach:

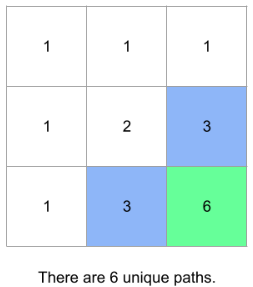
• create a 2D matrix to store value, which count that number of way to reach a certain (x,y) point. For example matrix[1][1] = 2 => from (0,0) -> (1,1) there are 2 ways.
• visualize the 2D matrix as tree: each node(x,y) is a cell in the matrix.
• using BFS to traverse the tree/ go to node/ go to cell and get the value at each node/cell.
• stop/ base condition : once matrix[1][1] is reached.

The following figure illustrates the value at the cells after completing flood fill/ BFS

The following are key points of BFS implementation:

• a queue is used to store currNode and two adjNode. Queue is FIFO.
  • initially the currNode and 2 adjNodes are pushed to queue.
  • run while loop, pop out the queue, one node in each iteration until the queue is empty.
  • process the value at the currNode = top_adjNode + down_adjNode.
  • then push in the next 2 adjNodes. Dont push it boundary of matrix or destination cell is reached.
• return the value of the destination cell.

Code Implementation:

class Solution {
    int bfs(int m, int n){
        vector<vector<int>> matrix (m, vector<int> (n, 1));
        queue<pair<int,int>> nodePaths;
        nodePaths.push({0,0});
        while (!nodePaths.empty()){
            pair<int,int> currNode = nodePaths.front();
            nodePaths.pop();
            //update value of currNode, which is the count of paths arriving this cell from {0,0}
            // case 1: cell is at top row or left column, the path from (0,0) to it is always 1
            // case 2: cell is elsewhere, value is added from topAdj and leftAdj
            int row = currNode.first;
            int col = currNode.second;
            if( row != 0 || col != 0){
                matrix[row][col] = matrix[row][col-1] + matrix[row-1][col];
            }
                     
            // check boundary before going to next node.
            if ( row+1 < m){
                pair<int,int> leftAdjNode  = make_pair(currNode.first+1, currNode.second);
                
            }
            if ( col <n){
                pair<int,int> rightAdjNode = make_pair(currNode.first,currNode.second+1);
                pair<int,int> leftAdjNode  = make_pair(currNode.first+1, currNode.second);
                nodePaths.push(rightAdjNode);
                nodePaths.push(leftAdjNode);
            }
            
        }
        return matrix[m-1][n-1];
    }
public:
    int uniquePaths(int m, int n) {
        // create a matrix to store value, which count that number of way to reach a certain (x,y) point
        // matrix[1][1] = 2 => from (0,0) -> (1,1) there are 2 ways. 
        // visualize it as tree: each node(x,y) is a cell in the matrix. 
        // using BFS to traverse the tree/ go to node/ go to cell and get the value. 
        // stop/ base condition : once matrix[1][1] is reached.
            return bfs(m, n);
    }
};

Optimization

• Redundant Queue Entries: The first program pushes both right and down adjacent nodes into the queue without checking if they have been visited before. This can lead to multiple entries of the same node in the queue, significantly increasing memory usage.
• Matrix Updates: The first program updates the matrix values without proper boundary checks, which can lead to unnecessary updates and increased memory usage.

The complexity of an optimized BFS should be:

• Time complexity: O(MxN)
• Space complexity: O(MxN)

Iteration - Bottom Up approach.

#include <vector>

using namespace std;

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m, vector<int>(n, 1));
        
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        
        return dp[m - 1][n - 1];
    }
};