Introduction
Indian computer scientist Jay Kadane in 1984 develop Kadane 's algorithm to solve the famous Maximum Subarray problem. In this post, I describe about the famous problem and its solution, using Kadane algorithm. I also attempt to solve other similar problems using the same techniques.
Concepts
- Continous subarrays form from adjacent elements of original array. Various question evolves around continuous subarray such as finding maximum sum, maximum product of continuous subarray.
- Kadane algorithm questions if the subarray should be grow up or should it be drop and restarted with basic subarray.
I will use the Maximum Subarray to elaborate about the basic concept behind Kadane's algorithm
Basic take-home ideas:
- The subarray sum is added by continuous items. If the sum is less than zero, the subarray is not worth considered, reset the sum to the value at the current index, and restart of the subarray.
currentSubarray = max(nums[i], currentSubarray + nums[i]);
- The initial value of the subarray is at index zero, so is the sum.
Code implementation:
int maxSubArray(vector<int>& nums) {
// Initialize our variables using the first element.
int currentSubarray = nums[0];
int maxSubarray = nums[0];
// Start with the 2nd element since we already used the first one.
for (int i = 1; i < nums.size(); i++) {
// If current_subarray is negative, throw it away. Otherwise, keep
// adding to it.
currentSubarray = max(nums[i], currentSubarray + nums[i]);
maxSubarray = max(maxSubarray, currentSubarray);
}
return maxSubarray;
}Problem Best time to buy stocks
Intuitive one-pass approach
This approach is more like greedy. I observe the entire price charts:
- For any buy day, so long the price on the following days are higher, there is profit. We could track the max profit of buy-sell after a certain buy day.
bestProfit - The best buy day has the lowest prices. In other words, for any sell day, the best profit is achieved by keeping track of the best buy day with
minPrice - It is possible that the best day with minPrice, may not be followed by good sell day, but we already store and keep track of
bestProfit

- The problem is solved by keeping track of
minPriceandbestProfit. - Note that the starting index is 0. We will take the price of the first day as
minPrice,
Code implementation:
int maxProfit(vector<int>& prices) {
int bestProfit = 0,
int minPrice = INT_MAX;
for(int i = 0; i < prices.size(); i++) {
// keep track of the best buy day so far
minPrice = min(prices[i], minPrice);
// keep track of the best profit
maxProfit = max(maxProfit, prices[i]-minPrice);
}
return maxProfitSoFar ;
}Kadane approach
The problem, could be solved with other algorithms. But since the input is an array of prices, and the continuous buy sell could be represented as the sum of a subarray, this problem could be solved with Kadane's algorithm. However, it is a bit tricky since we have to make subtraction for buy case, and have to make subtraction before any addition (sell).
- Think of
currentProfitas continuous subarray of size 2 wherecurrentProfit[i]= price[today]-price[yesterday]. - However, since we have bad days, where currentProfit is negative, we need to discard such days. In other words, we discard the subarray whose sum is negative.
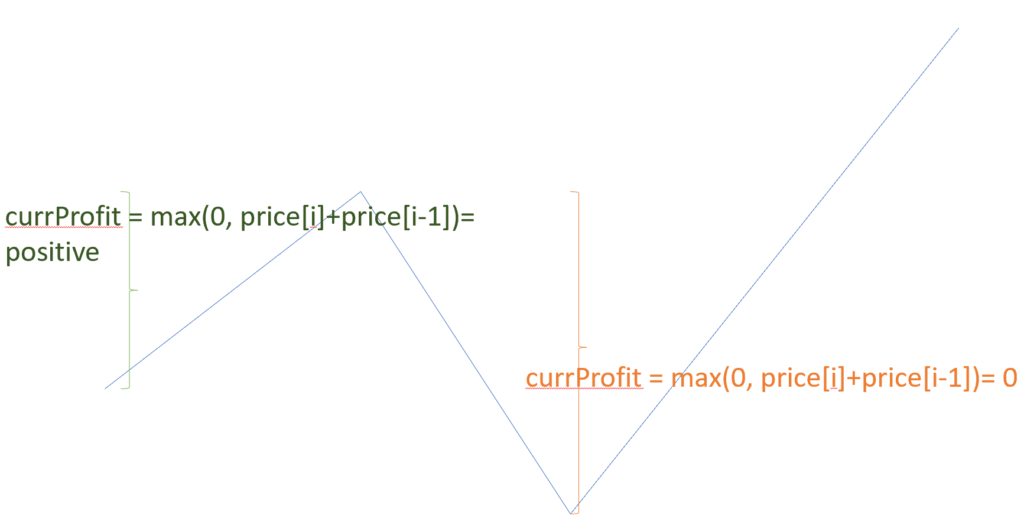
- Consequently
currentProfitis achieved by comparing betweenzeroand+= prices[today]- prices[yesterday].currentProfitis initialized to zero. - among all the subarrays of size 2, we keep track of the maximum subarray,
bestProfitSoFar - Note that the starting index is 1.
Code implementation
int maxProfit(vector<int>& prices) {
int curProfit = 0, maxProfitSoFar = 0;
for(int i = 1; i < prices.size(); i++) {
curProfit = max(0, curProfit += prices[i] - prices[i-1]);
maxProfitSoFar = max(maxProfitSoFar , curProfit );
}
return maxProfitSoFar ;
}Problem Maximum Product Subarray
The problem Maximum Product Subarray is best approach with subarray array concept and Kadane algorithm:
- subarray are continuous arrays, whose
currProduct *= nums[i]. - Kadane algorithm says that the subarray should be reset if the product goes
zero. Thus we have:
currProduct = max( nums[i], goodProduct).The value goodProduct needs more logic consideration here. It will be positive if:
nums[i]is negative and previous accumulated product is negative. We want to optimize this product with a min value, because it potentially make maximum product. Thus we keep track ofmin_so_far.nums[i]is positive and previous accumulated product is positive. We want to optimize this product with a max value. Thus we keep track ofmax_so_far.
How to calculate min_so_far and max_so_far:
min_so_faris the min value of- current value
num[i]if it is negative. Kadane concept kicks in again. We want to reset the product if it goes positive. - otherwise, it is min between
(num[i]*min_negative_product). - the reason behind keeping track of
min_so_faris to properly handle negative numbers.
- current value
min_so_far = min(num[i], min(max_so_far * num[i], min_so_far * num[i]));max_so_faris the max:- current value
nums[i]. Kadane concept again. - otherwise, it is max between
(num[i]*max_positive_product). - The reason behind keeping track of
max_so_faris to keep track of the accumulated product of positive numbers
- current value
The following illustrates the scenario when max_so_far is reset to nums[i]=-5 while min_so_far is updated as the most negative found:
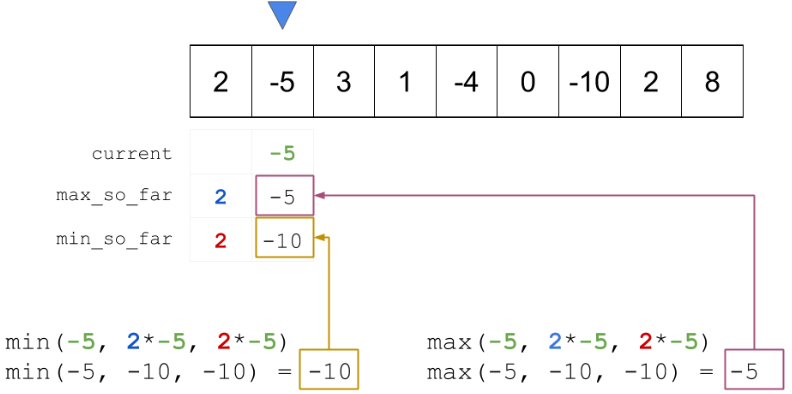
The following illustrates how the min_so_far negative value becomes that max product when it is multiply with numbs[i]=-4:

Caution: currProduct has a role in calculating min_so_far or max_so_far, depending on code setup. Without it, the solution will be wrong!!! For the above logic, (suggested by Leetcode Editorial), we have to:
- calculate currProduct
- update
max_so_farwith currProduct.
Code Implementation:
class Solution {
public:
int maxProduct(vector<int>& nums) {
int max_so_far = nums[0];
int min_so_far = nums[0];
int result = max_so_far;
for (int i = 1; i < nums.size(); i++){
int current = nums[i];
// currProduct the product of current subarray.
// currProduct is reset to nums[i] if the product goes negative or zero.
int currProduct = max (current, max (max_so_far*current, min_so_far*current));
min_so_far = min (current, min (min_so_far*current, max_so_far*current));
// must update max_so_far after min_so_far
max_so_far = currProduct;
result = max (max_so_far, result);
}
return result;
}
};Problem Max subarray sum with length divisible by K
This problem Maximum Subarray Sum With Length Divisible by K can use continuous subarray sum concept; therefore, the following should be considered using together: prefix sum array and Kadane algorithm.
Prefix sum array:
- the prefix sum arrays accumulate the sum of each item from index=0 in the original array.
- for any subarray start at
index=iand ending atindex=j, the subarray sum is calculated byprefixSum[j] - prefixSum[i-1]

Kadane algorithm
Kadane algorithm asks if we could grow our subarray to some multiples of k or reset it to the basic subarray whose length is k.
- We have
currSubarraySumis the sum of subarray that either has length of k or not divisible by k. Thus we havecurrSubarraycalculated as. In other words,currSubarrayis the basic subarray sum that we would reset to.
long long currSubarraySum;
if (i == k-1) // subarray ending at index i, not divisible by k
currSubarraySum = prefix_sum[i]
else // length is divisible by k, subarray ends at index i
currSubarraySum = prefix_sum[i] - prefix_sum[i-k]; - We store the
currSubarraySumto a vectorsubArraySum.- Applying Kadane algo, we can decide to grow subarray to any multiple of k. Or we reset the subarray to the basic subarray sum, that we reset to.
- at any
index = iwe compare:- the sum of basic array whose length is k , thus the starting index is
i-k. The sum iscurrSubarraySum = prefix_sum[i] - prefix_sum[i-k] - the subarray starting index is
i - k
- the sum of basic array whose length is k , thus the starting index is
The following illustrates the consideration when index=4 and k=2. We compare the sum between subarray {-3,4} and subarray {1,2,-3,4}

Thus we have the following codes:
subArraySum[i % k] = max(subArraySum[i%k] + currSubarraySum , currSubarraySum );Caution: Iteration loop doesn't start at index =0. Instead it should starts at index k-1. Basically, we want the subarraySum vector to stored the sum of our target subarrays, lengh is k or some multiple of k.
The following solution are provided by fergalicrizz - LeetCode Profile . I change the variable names to fit with the explanation here.
class Solution {
public:
long long maxSubarraySum(vector<int>& nums, int k) {
int n = nums.size();
vector<long long> prefixSum(n);
prefixSum[0] = nums[0];
for (int i = 1; i < n; i++) {
prefixSum[i] = prefixSum[i - 1] + nums[i];
}
long long small_const = -1e18;
// subArraySum[i] holds the Kadane best prefix for things that are i mod k.
vector<long long> subArraySum(k, small_const);
long long res = small_const;
for (int i = k - 1; i < n; i++) {
long long currSubarraySum = (i == k - 1) ? prefixSum[i] : prefixSum[i] - prefixSum[i - k];
subArraySum[i % k] = max(subArraySum[i % k] + currSubarraySum, currSubarraySum);
res = max(res, subArraySum[i % k]);
}
return res;
}
};