Sort Algorithm 1 – Selection vs Bubble vs Insertion Sort

Introduction

I review basic Sorting techniques by comparing similar algorithms. Sorting is something developers like me usually forgo due to availability of C++ provided standard functions. Yet, no knowledge should be ignored.

I also find that the simple memorization of big O notation for each type of algorithm not sufficient to fully understand nor help with recalling correct complexity.

While there are many ways to implement the algorithm, I tried to use similar pattern, that is using double nested loops so that I could reveal nuance different between those techniques.

Thus in this blog, I review some basic concepts of sorting, deriving complexity for nested for loops and then distinguish the differences between Selection, Bubble and Insertion Sort.

Stable vs Not stable sort

Stable sort should not rearrange equal items. or example consider the collection [4, 2, 3, 4, 1]. After the first round of selection sort, we get the array [1, 2, 3, 4, 4]. This array is sorted, but it does not preserve the ordering of equal elements. (Source: Leetcode).

Calculating time complexity of nested for loop

For the following for nested for loop, where both counters begin at zero and end at the max size:

for (int i = 1; i <= n; i++ ) {
    for (int j = 1; j <= n; j++ ) {
          cout<<"j"<<endl;
    }
}

The inner for loop executes n times.
The outer for loop also executes n times.
Thus the total time that the codes execute is n*n total operations. Time complexity is O(n^2).

For the scenario when the outer loop counter starts at zero, while the inner loop counter starts at the value of the outer loop counter, we have:

for (int i = 1; i <= n; i++ ) {
    for (int j = i; j <= n; j++ ) {
          cout<<"j"<<endl;
    }
}

When i = 1, the inner loop runs from j = 1 to j = n, which is n iterations.
When i = 2, the inner loop runs from j = 2 to j = n, which is n - 1 iterations.
When i = 3, the inner loop runs from j = 3 to j = n, which is n - 2 iterations.
This pattern continues until i = n, where the inner loop runs only once.

The total number of iterations of the cout << "j" << endl; statement is the sum of the series n+(n−1)+(n−2)+…+1n + (n-1) + (n-2) + ... + 1 or

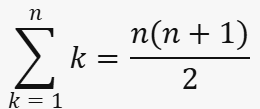
The above 2 codes would apply for Selection and Bubble Sort.

Selection sort vs Buble sort

The following compares 2 techniques, assuming that they are to be used to sort items in ascending order.

	Selection Sort	Bubble Sort
Basic strategy	Loop through the array, find the smallest items and place them in its correct position.	Continuously swap 2 adjacent items until there is no item to be swapped. Basically move the largest item to top.
Pseudo code	outer loop: i=0 to i = array.size pick item array[i] inner loop: j=i+1 to i=array.size look for smallest item swap with item array[i]	set swap = false; outer loop: i=0 to i = array.size inter loop: i=0 to i<array.size -i-1 swap to adjacent items set swap to true if (swap==false) break;
Time complexity	O(n^2)	O(n^2) but potentially O(n) in best case scenario due to the the inner loop has to be fully run at least once. Slightly faster than Selection Sort in normal case.
Space complexity	O(1) due to temp item	O(1) due to temp item

Animation for Selection Sort:

Animation for Bubble Sort:

Code implementation for Selection Sort:

 void selectionSort(vector<int> &arr){
        int min_index;
        for (int i = 0; i < arr.size(); i++) {
            min_index = i;
            for (int j = i + 1; j < arr.size(); j++) {
                if (arr[j] < arr[min_index]) {
                    min_index = j;
                }
            }
            // Swap current index with minimum element in rest of list
            int temp = arr[min_index];
            arr[min_index] = arr[i];
            arr[i] = temp;
        }
}

Code implementation for Bubble Sort:

void bubbleSort(vector<int>& arr) {
        bool hasSwapped = false;
        for (int i = 0; i < arr.size()-1; i++){
            for (int j = 0; j <arr.size()-i-1; j++){
                if (arr[j]> arr[j+1]){
                    // swap
                    int temp = arr[j];
                    arr[j]  = arr[j+1];
                    arr[j+1]= temp;
                    hasSwapped = true;   
                }
            }
            // if there is a single item that needs to be swapped, then loop all the way.
            // if there is no item to be swapped in the 1st iteration => best scenario
            if (!hasSwapped){
                break;
            }
        } 
}

Insertion Sort

Insertion sort is intuitively remembered as picking an item, and compare it with all previous (left) item. Swap the items if needed. Place the item to its correct position, for small value in the left.
Time complexity is O(n^2), where best case scenario is O(n).
- Worst case scenario is when the input list is completely reversed. Total operations are calculated as 1+2+…+(n−1)1+2+…+(n−1)
- Insertion sort is stable sort. Equal items shouldn't be swapped.
Space complexity is O(1)

Code implementation for Insertion Sort:

#include <iostream>
#include <vector>
using namespace std;

void insertionSort(vector<int>& arr) {
    int i, j, key;
    for (i = 1; i < arr.size(); i++) {
        key = arr[i];
        for (j = i - 1; j >= 0 && arr[j] > key; j--) {
            arr[j + 1] = arr[j];       // shift value to the right if the key is smaller.
        }
        arr[j+1] = key;      // place the key (small value) to the its correct position, 
    }
}

int main() {
    vector<int> arr = {2, 4, 5, 1, 6, 0, 1, 10, 9};
    insertionSort(arr);
    for (auto i : arr) {
        cout << i << " ";
    }
    cout << endl;
}

Animation for Insertion Sort:

Conclusion

The above algorithm should only be used for small input due to high time complexity.
Robust sort function should check for size.
Only Bubble Sort and Insertion Sort are stable, Thus equal comparison shouldn't be used.
Comparison sort may need comparison operator overload defined.